PYRAX® Bemessungsregeln

Das patentierte PYRAX^®-Blech mit den schachbrettartig angeordneten Pyramidenstumpfe wurde für das Übertragen von biaxialen Querkräften quer und längs zur Arbeitsfuge entwickelt. Die schachbrettartig PYRAX^®-Technologie erlaubt einen hohen Querkraftwiderstand von mindestens 85% eines monolytischen Stahlbetonbauteils ohne Biegebeansprung. Die Bemessung der PYRAX^® Fuge erfolgt über die Biege- und Querkraftnachweis der Norm SIA 262.

Mit der speziell abgestuften Geometrie erreichen Fugen mit der PYRAX^®-Technologie einen wesentlich höheren Anteil an Grundfläche der Verzahnung bezüglich der Gesamtfläche. Zudem wird durch die schachbrettartige Anordnung der Verzahnungsnocken eine richtungsunabhängige Schubkraftübertragung erreicht. Das PYRAX^®-Blech ist vielseitig und bildet die Grundlage von vier verschiedenen Produktvarianten.

Bemessungsgrundlage und Normenbezug

Die Bemessungswiderstände der PYRAX^® Fuge werden grundsätzlich mit den Bestimmungen der Norm SIA 262 (2013) Art. 4.3.2 und 4.3.3 über die Biege- und Querkraftbemessung ermittelt.

Bauteile OHNE Querkraftbewehrung (Platten (Decken))

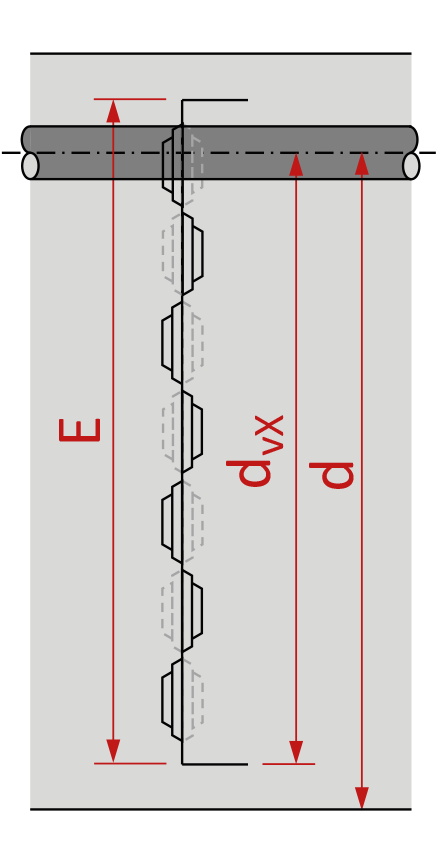
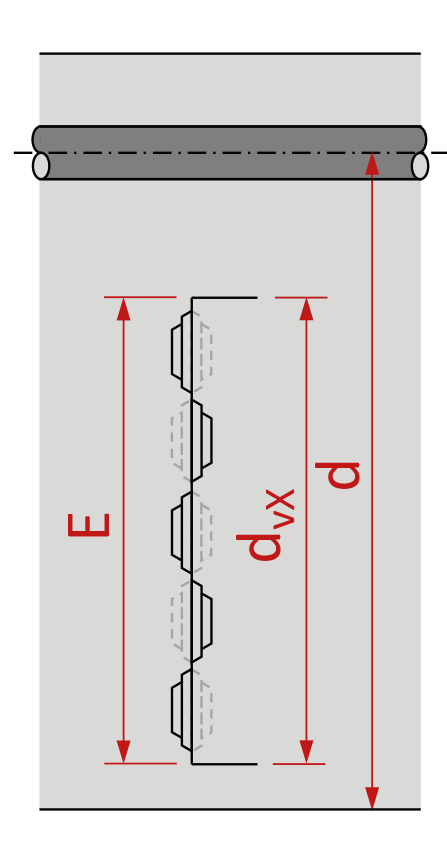
Für die Bestimmung des Querkraftwiderstands ist Art. 4.3.3.2 der Norm SIA 262 massgebend. Versuche an Plattenstreifen mit PYRAX^® Fugeneinlagen mit vollflächiger Verzahnung zeigten keine Reduktion des Querkraftwiderstands verglichen mit Plattenstreifen ohne Einlagen. Damit gelten für den Querkraftnachweis der PYRAX^® Fuge der unveränderte Materialkennwert τ _cd,X = 1.0 τ_cd sowie die Faktoren k_d nach Gl.(36)₂₆₂ und kg nach Gl.(37)₂₆₂. Die für die Aufnahme der Querkraft in der Fuge wirksame statische Höhe d_vX ist gemäss Abb.1 und Abb.2 mit Berücksichtigung der Blechabmessungen zu bestimmen.

Der Querkraftwiderstand einer Platte (Decke) berechnet sich in der PYRAX^® Fuge damit zu

v_Rd,X = k_d • τ_cd,X • d_vX [kN/m]

(35)₂₆₂

τ_cd,X =1.0 τ_cd
k_d : Gl.(36)₂₆₂ ; mit k_g = 1.0 für D_max 32mm
d_vX = für die Querkraftübertragung wirksame verzahnte
statische Höhe; d_vX ≥ E vgl. Abb. 1,2

(0)_PYRAX®

• Üblicherweise Abstand von der Zugbewehrung bis zur gegenüberliegenden Blechkante (Abb 1).
• Bei Teilverzahnung des Querschnitts darf für d_vX maximal die Blechbreite E eingesetzt werden (Abb. 2).

Zur Bestimmung des Biegewiderstands ist in der Druckzone die unverminderte Betondruckfestigkeit f_cd gültig.

Bemerkungen für Fugen bei Auflagern

• Bezüglich unterer Plattenbewehrung im Auflagerbereich wird speziell auf Art. 5.5.3.3₂₆₂ verwiesen.
• PYRAX^® Fugen ohne Bewehrung auf der Zugseite sind grundsätzlich nicht zulässig.

Bauteile MIT Querkraftbewehrung (Scheiben (Wände), Platten (Decken))

Der Querkraftwiderstand der PYRAX^® Fuge erreicht durch die patentierte Verzahnung in Versuchen rund 85% des homogenen Betons. Dies kann durch eine entsprechende Reduktion der Betondruckfestigkeit im Fugenbereich mit dem Faktor k_X berücksichtigt werden. Für die Bemessung wird im Spannungsfeld die Betondruckfestigkeit mit dem k_X-Faktor auf 80% begrenzt.

f_cd,X = k_X • f_cd mit k_X = 0.8

(1) _PYRAX®

Zur Bestimmung des Biegewiderstands ist für Druckzonen, welche senkrecht zur Fuge laufen die unverminderte Betondruckfestigkeit f_cd gültig.

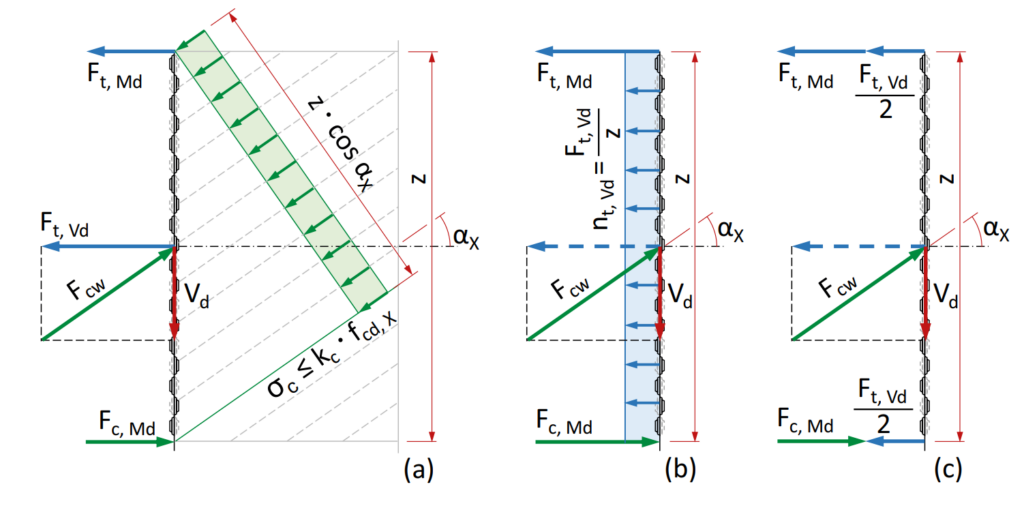
Fugen mit parallelem Spannungsfeld

Die Querkraft wird durch ein geneigtes Spannungsfeld mit der resultierenden Druckkraft F_cw übertragen. Deren Vertikalkomponente steht mit der Querkraft V_d im
Gleichgewicht, deren Horizontalkomponente mit der Zugkraft F_t,Vd (Abb. 3).

Diese Zugkraft ergibt sich mit vertikalen Bügeln zu
F_t,Vd = V_d • cotα_X [kN]

(50)₂₆₂

Der maximale Querkraftwiderstand in der PYRAX^® Fuge (Scheiben (Wände), Platten (Decken)) wird durch die Betonfestigkeit k_c • f_cd,X im Spannungsfeld begrenzt auf
(Abb. 3 (a))

Scheiben (Wände):
V_Rd,cX = b_w • z • k_c • f_cd,X • sinα_X • cosα_X [kN]

(45)₂₆₂

Platten (Decken):
v_Rd,cX = z • k_c • f_cd,X • sinα_X • cosα_X [kN/m]

(2) _PYRAX®

b_w = Wanddicke, maximal die verzahnte Dicke (b_w ≤ E)
z = Hebelarm innere Kräfte, maximal die verzahnte
Höhe (z_Platten ≤ E resp. z_Scheiben ≤ L)
kc = 0.55 bzw. k_c=0.40 bei plastischer Zuggurtdeformation
f_cd,X = k_X • f_cd mit k_X=0.8, vgl. Gl.(1)_PYRAX®

Das Kräftepaar F_t,Md und F_c,Md ergibt sich aus dem Biegemoment M_d und dem Hebelarm z zu:

F_t,Md = F_c,Md= \(\frac{ |M_{ d }| }{ z }\) [kN]

(3) _PYRAX®

Im Falle einer Scheibenfuge (Wände) wird die Zugkraft F_t,Vd üblicherweise mit einer auf die Höhe z verteilten Horizontalbewehrung übernommen (Abb. 3(b)). Für z darf maximal die verzahnte Höhe eingesetzt werden. Die verteilte Zugkraft ist:

n_t,Vd = \(\frac{ F_{ t,Vd } }{ z }=\frac{ V_{ d } }{ z }\) • cotα_X [kN/m]

(4) _PYRAX®

Im Falle einer Plattenfuge (Decken) wird die Zugkraft F_t,Vd entsprechend der Angabe in Art. 4.3.3.4.12₂₆₂ üblicherweise je hälftig auf den Zug- und Druckgurt aufgeteilt (Abb. 3(c)). Die resultierenden Kräfte im Zug- und Druckgurt sind dementsprechend:

F_t= \(\frac{F_{t,Vd}}{2}+\frac{|M_{d}|}{z}\)

(5a) _PYRAX®

F_c= –\(\frac{F_{t,Vd}}{2}+\frac{|M_{d}|}{z}\)

(5b) _PYRAX®

Für ein geringes oder verschwindendes Biegemoment kann die Kraft F_c negativ werden (Zugkraft) was auch hier eine Bewehrung bedingt.

Der notwendige Bewehrungsquerschnitt ist:

A_sX = \(\frac{F_{t}}{f_{sd,X}}\) [mm²] bzw. für die verteilte Kraft n_t,Vd

a_sX,Vd = \(\frac{n_{t,Vd}}{f_{sd,X}}\) [mm²/m]

(6)_PYRAX®

f_sd,X = Bemessungswert der PYRAX^®-Bewehrung

Fugen bei Auflagern

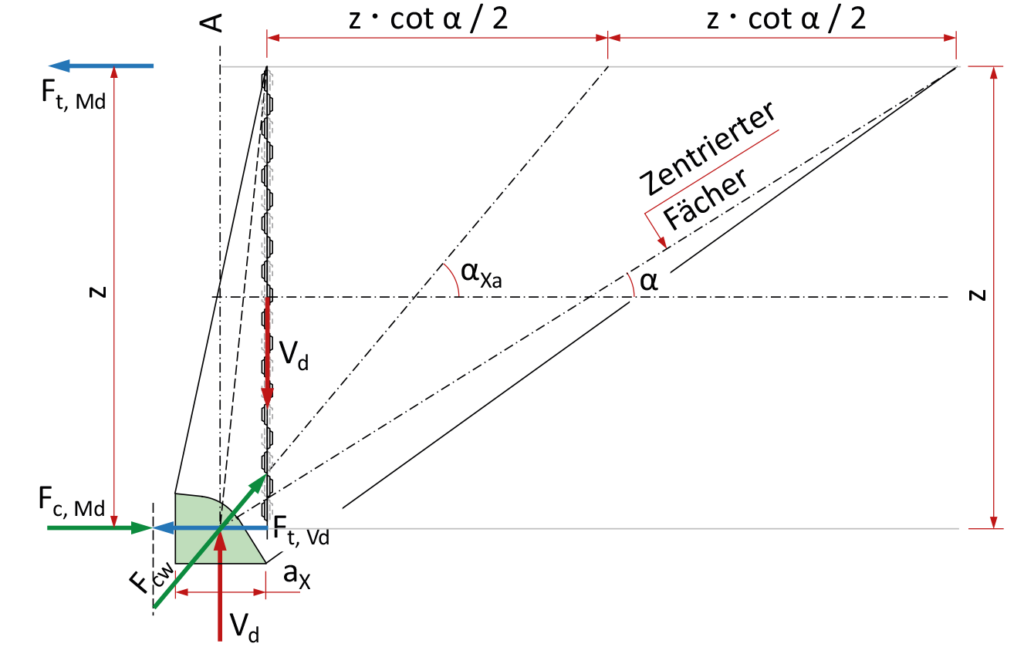
Für eine PYRAX^® Fuge im Bereich eines Auflagers in Bauteilen mit Querkraftbewehrung (Abb.4, direkte Auflagerung) gilt Art. 4.3.3.4.1₂₆₂. Der Querkraftnachweis erfolgt im Abstand z•cotα vom Auflagerrand nach der Gleichung (45)₂₆₂ mit der Betonfestigkeit f_cd,X .

Die Zugkraft F_t,Vd in der Fuge wird anhand der Achsneigung α_Xa des auf der Auflagerlinie zentrierten Fächers bestimmt (Abb. 4).

Die Zugkraft F_t,Vd wirkt im Fugenquerschnitt am Durchstosspunkt der Fächerachse. Vereinfacht wird F_t,Vd gesamthaft dem Untergurt zugeordnet und dementsprechend der Nachweis der Bewehrung direkt im Auflagerschnitt A geführt. Für Fugen mit auf einen Teilquerschnitt beschränkter Verzahnung sind dementsprechende Spannungsfeld-betrachtungen vorzunehmen.

Der Bereich hinter dem Auflager ist gesondert zu betrachten. Insbesondere sind die Platzverhältnisse für die Druckstreben und die Verankerung der Bewehrung zu prüfen. Zur Bestimmung der Strebenabmessungen wie auch der Auflagerbreite a_X gilt die Betonfestigkeit f_cd.

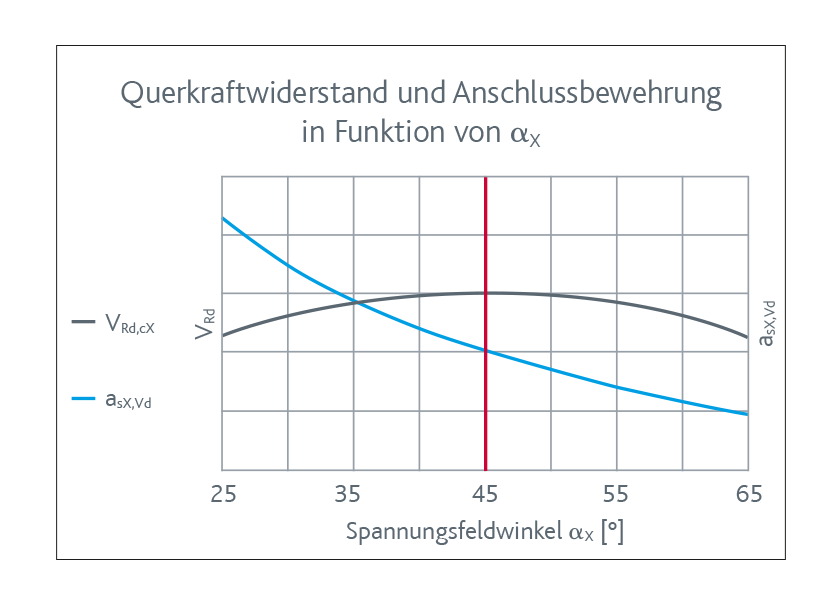
Spannungsfeldwinkel α_x , Querkraftwiderstand und Anschlussbewehrung

Der Spannungsfeldwinkel α_X kann durch den Ingenieur im Rahmen der Grenzwerte aus der Norm SIA 262 festgelegt werden. Für die PYRAX^® Anschlussfugen wird empfohlen:

25° ≤ α_X ≤ 65°

(7)_PYRAX®

α_X=Winkel Fugensenkrechte zum Spannungsfeld

Der Querkraftwiderstand V_Rd,cX bzw. v_Rd,cX erreicht ein Maximum beim Spannungsfeldwinkel α_X = 45° (Abb. 5, graue Kurve).

Der erforderliche Bewehrungsquerschnitt a_sX,Vd der
Anschlussbewehrung nach Gl. (6)_PYRAX® nimmt mit zunehmendem Spannungsfeldwinkel α_X ab (Abb. 5, blaue Kurve).